The world is deeply, deeply strange.
And you can hold that strangeness in the palm of your hand.
Take a radioactive isotope of an element. We know the half-life of that element. But we cannot predict exactly when that individual atom will decay into its stable isotope. Group a bunch of radioactive atoms together, and after one half-life, we know that half of them will have decayed. But even knowing that, we cannot predict whether a particular atom in that group will decay during that half-life.
Put 1000 atoms in a block, we can tell you that in one half-life, exactly 500 atoms will have decayed. But we cannot tell you which ones.
This kind of weirdness is baked into our reality. There’s subtle effects, like Benford’s Law, but you may have literally held this weirdness.
Especially if you’ve ever played Catan.
If you roll a single six-sided die [1], you have an equal chance (16.6 repeating) of rolling any number. Each roll is entirely random. It’s the principle of independent probability. So far, so straightforward.
You can add a second six-sided die. Each roll of that second die is also completely random, with an equal chance of rolling any number.
But the moment you add the two die rolls together, you get something that isn’t random. You get something that looks like a normal distribution (the "bell curve"). [2]
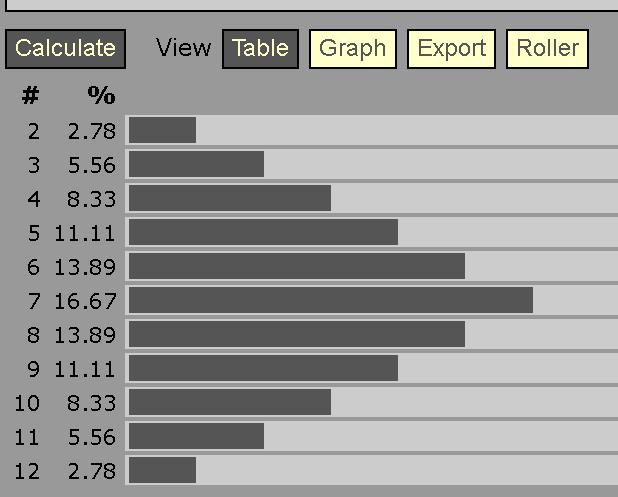
Something as simple as grouping changed the essential quality of those die rolls, from random to predictable. But without changing the rolls themselves.
Just the same way that collecting atoms of a radioactive isotope changes radioactive decay, collecting these other random values changes them into something predictable.
It’s easy to just shrug and blow past this kind of thing, but take a moment to really consider this.
That the way that something is looked at and grouped, the way they’re considered and thought about, transforms them from chaos into some kind of order… without altering the fundamental underlying randomness.
That transition demonstrates the fundamental strangeness of chaos theory, and even provides a metaphor [3] for the disconnect between our quantum and classical models of physics in way that lets us grok it, even if we can’t always do the math.
Once you’ve thought about all that, there’s a further thing to consider. If order emerges from randomness at the scale of grouped atoms, and also at the scale of rolled dice…does this effect continue to scale at all levels like Benford’s Law and other statistical strangeness? What does that possibly say about randomness and free will? Random actors and societal trends? And if it does not continue to scale, why not? What changes?
Featured Photo by Edge2Edge Media on Unsplash

[1] Assuming a Spherical Chicken (or cow).
[2] Technically it’s a triangular distribution, but the idea stands.
[3] At least a metaphor; this is about the limit of my understanding of the math and physics here, so I think it’s just a metaphor…
